True-RMS란 무엇일까요?
True RMS – The Only True Measurement

<그림 1 : One Current – Two Readings>
위의 그림은 같은 전선에 걸려있는 두 개의 클램프 미터[Clamp Meter]를 보여 주고 있다. 두 미터가 같은 전류치를 나타내어야 하지만 사진에서는 두 개의 다른 값을 각각 나타내고 있다.
어느 값이 진짜일까?
두 개의 미터는 기능상으로 전혀 문제가 없으며, 공장에서의 자체 시험을 통과한 제품이다. 단지 두 제품의 차이는 내부의 계측 방법이다. 왼쪽의 미터는 True RMS 계측 방식이며, 오른쪽의 미터는 평균치 계산을 통한 RMS 계측 방식이거나 기본파 성분 계산을 통한 RMS 계측 방식이다. 이러한 차이를 이해하기 위해서는 RMS가 무엇을 의미하는지 이해할 필요가 있다.
RMS란 무엇인가?
직류나 교류가 저항을 통하면 열이 발생한다. 순시치가 i A인 교류 전류가 저항 R을 통할 때 발생되는 열량과 동일한 열량을 발생시킬 수 있는 직류를 I A라고 하면 이 직류의 크기 I를 교류 전류 i의 실효치라고 한다. 따라서 가령 실효치 5A의 교류(정현파 전류가 아니라도 무방하다)와 5A의 직류는 같은 열 효과를 나타내며 또 실효치가 같다면 다른 형태의 주기전류도 같은 열효과를 나타낸다. 실 효치를 root mean square value, 약해서 RMS 혹은 r.m.s.치라고 하는데, 이것은 실효치가 교류 순시치의 제곱의 평균치의 평방근과 같기 때문이다.
이를 수식으로 표현하면 다음 식과 같다.

그러면 그림 2와 같은 완전한 싸인파(정현파)인 경우 RMS치는 얼마일까?
RMS 값은 피크(최대)값의 0.707배이고, 반대로 말하면 피크값은 RMS의 √2 혹은 1.414배이다. 즉 완전한 정현파인 경우 RMS 치가 1A라 하면 피크값은 1.414A이다. 또한 부의 부분을 뒤집어 정류된 파형의 평균치를 구하면 피크값의 0.636배이고 RMS의 0.9배이다. 이러한 관계에 의하여 아래와 같은 요소를 정의하고 구할 수 있다.


<그림 2 : 완전한 정현파(pure sinewave)>
여기에서 측정하고자 하는 파형이 완전한 정현파라고 하면(완전한 정현파라는 조건이 중요 하다) 신호를 정류하고 평균치를 구한 다음 1.111을 곱하거나 피크치를 구하여 여기에 0.707을 곱한 값을 RMS치(실효치)라고 하여도 아주 정확한 값이다. 이러한 계측 방법은 아날로그 미터를 포함하여 대부분의 디지털 전압, 전류계에서도 이용되고 있으며 ‘평균값 계측에 의한 RMS 교정 : mean reading, RMS calibrated’ 방식이라고 한다.
이 방식의 문제는 완전한 정현파가 전기가 사용되는 실제 세상에 존재하지 않는다는 점이다.
그림 3의 파형은 PC에 인입되는 전류파형의 예이다. True RMS 값은 그림 2와 같이 1A이 지만, 피크치는 그림 2의 경우 보다 훨씬 큰 2.6A이고, 평균값은 그림 2 보다 작은 0.55A 이다.
‘평균값 계측에 의한 RMS 교정 : mean reading, RMS calibrated’ 방식으로 제작된 메타는 평균치를 계측한 다음 1.111을 곱한 값을 RMS 값으로 표시하므로 0.55 x 1.111 = 0.61A로 표시되며 이는 True RMS 보다 거의 40% 작은 값이다.

<그림 3 : PC에 인입되는 전류파형의 한 예>
RMS 계산의 예
계측 방법에 따라 계측치의 편차가 나는 것을 보이기 위해서 다음과 같이 좀 더 간단한 파형을 예로 들었다.
<그림 4 : 기본파에 3조파가 더해진 파형의 예>
그림 4는 60Hz의 싸인파와 3조파인 180Hz의 싸인파를 합성한 파형을 나타낸 것이다. 파형 1은 60Hz와 180Hz가 동상인 경우의 합성 파형이고, 파형 2는 90º의 위상차가 있는 경우의 합성 파형이다. 이를 수식으로 표현하면 다음 식과 같다.
파형 1 : V(t) = 170*Sin(377*t) +50*Sin(1131*t)
파형 2 : V(t) = 170*Sin(377*t) +50*Cos(1131*t)
이러한 파형을 계측할 경우, 일부 저가의 디지털 메타는 파형을 정류한 다음 피크치를 검출한 다음 0.707을 곱하여 RMS 치로 표시한다. 앞서 언급한 것처럼 파형이 순수한 60Hz 정현파라면 이 값이 정확하지만, 3조파가 포함된 이 예에서는 다음과 같이 엉터리 값을 계측 하게 된다.
파형 1 : 203 x 0.707 = 144 V
파형 2 : 155 x 0.707 = 110 V
또한 고가의 판넬 메타나 복합계전기에서도 고조파 함유량에 관계없이 기본파 파형의 피크치를 계산한 다음 0.707을 곱하여 RMS로 표현하는 경우가 많다.
이 경우의 계측값은 두 파형 모두 다음과 같이 계산된다.
170 x 0.707 = 120.19 V
이 경우에는 고조파의 위상에는 영향을 받지 않으나, 고조파 함유량이 많을수록 계측 오차가 증가하므로 정확한 계측기기로 사용할 수 없다.
이와 같은 방법으로 계측하는 메타는 제작과정이나 교정과정에서는 그 오차를 알 수 없다. 제작하고 교정하는 과정에서 메타의 전압, 전류 입력을 제공해 주는 기기들은 거의 이상적인 정현파 파형을 제공해 주기 때문이다.
그럼 정확한 True RMS 값은 얼마인가?
앞서 True RMS의 정의를 ‘교류 순시치의 제곱의 평균치의 평방근’이라고 소개하였다. 이를 주파수를 기준으로 True RMS를 정의하면 ‘각 조파의 RMS 치의 제곱한 값들을 더한 값의 평방근’이다. 이 정의에 따라서 그림 4의 파형의 True RMS를 구하면 위상에 관계없이 두 파형 모두 다음과 같이 계산된다.

일반화를 시켜보면 다음과 같다.
V(t) =V1sin(wt +a1) +V2 sin(2wt +a 2) +V3sin(3wt +a3) +•••+Vm sin(mwt +a m)
m : 고조파 최대차수
ω : 기본파의 주파수
기본파 RMS 계산

고조파를 포함한 True RMS 계산
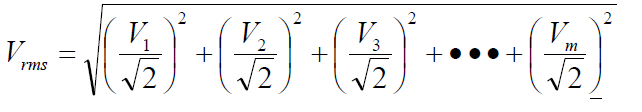
이와 같이 정확한 True RMS 값을 계측하기 위해서는 입력 전압, 전류 파형에 포함된 고조파 성분들이 정확히 반영되어야 한다.
이를 실제 현장에서 쉽게 체험할 수 있는 방법은 밧데리 충전기와 같이 파형이 많이 왜형된 입력전류가 흐르는 곳의 전류를 측정해 보면 된다.
또한 전력적인 측면에서 고려해보면 전압과 전류의 왜곡이 동시에 발생되는 실제 현장에서 의 전력값은 계측하는 방법에 따라 전압과 전류의 실효치보다 더욱더 큰값의 차이를 초래하 게 된다.
전압, 전류식
V(t) =V1sin(wt +a1) +V2 sin(2wt +a 2) +V3sin(3wt +a3) +•••+Vm sin(mwt +a m)
I(t) = I1sin(wt +b1) + I2sin(2wt +b2) + I3sin(3wt +b3) +•••+ Im sin(mwt +bm)
기본파 전력계산
고조파를 포함한 전력계산
전력 차이
특히 Digital 전력 계측 기기의 효용성 중에 가장 중요한 전력에 관련 계측은 기본 파와 더불어 고조파까지 고려되어야 한다.
[참고문헌]
1. Power Quality Application Guide : Harmonics, Copper Development Association
2. Measuring RMS Value of Voltage and Current, AN101, Dataforth Corporation